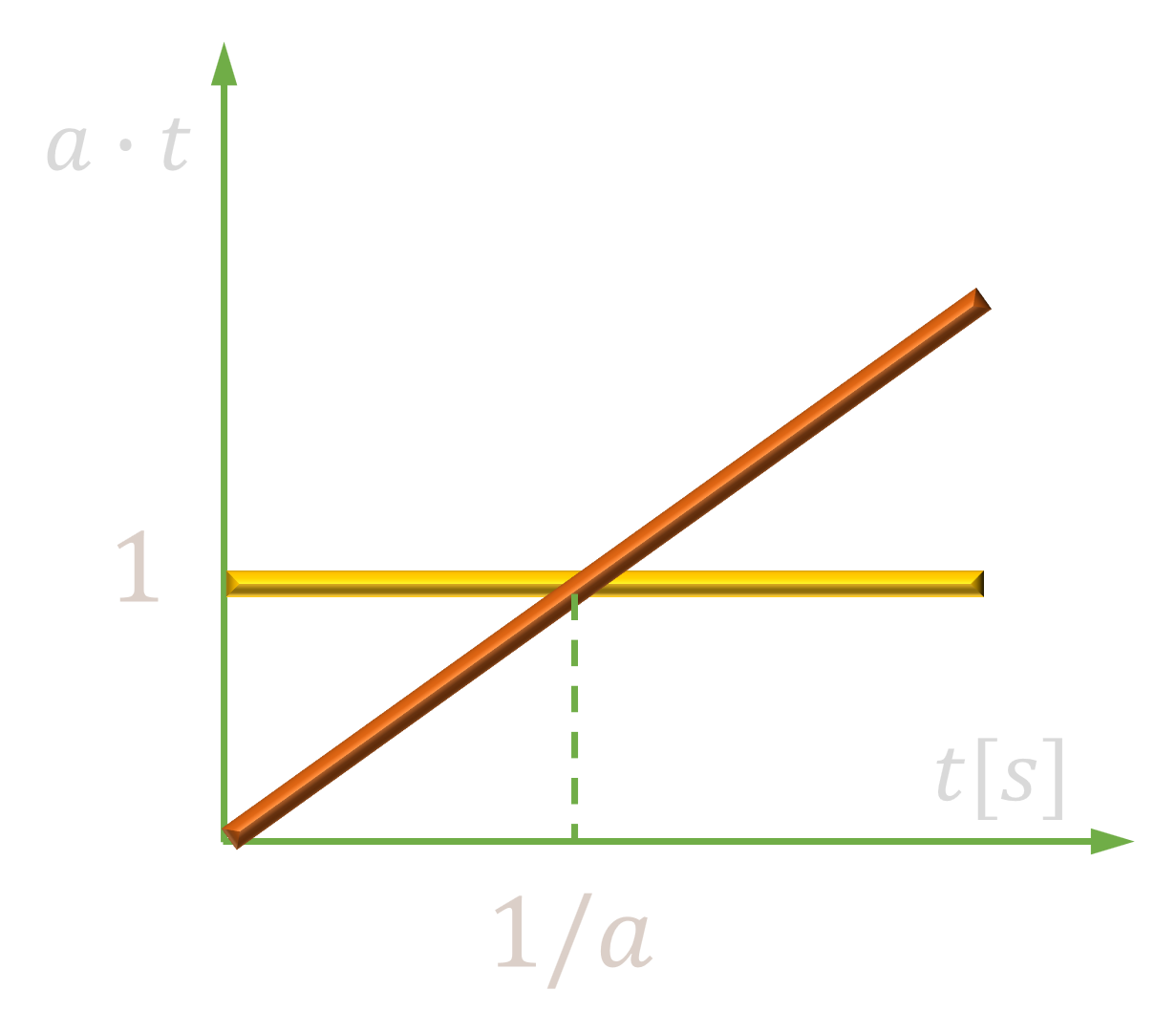Automatyka i robotyka należą do jednych najszybciej rozwijających się dziedzin techniki. O stopniu rozwoju technologicznego danej gospodarki świadczy m.in. jej zautomatyzowanie i zrobotyzowanie, co przekłada się na konkurencyjność na rynkach światowych. [1]
Automatyzację można ogólnie zdefiniować jako proces wykonywania z góry ustalonej sekwencji operacji przy niewielkim udziale pracy ludzkiej lub bez jej udziału, z wykorzystaniem specjalistycznego sprzętu i urządzeń, które wykonują i kontrolują procesy produkcyjne. Automatyzację procesu można osiągnąć poprzez zastosowanie różnorodnych urządzeń tj. czujniki, siłowniki i sterowniki, które są w stanie obserwować proces produkcyjny, podejmować decyzje dotyczące zmian, które należy wprowadzić w operacji oraz kontrolować wszystkie jego aspekty. Automatyzacja jest procesem w przemyśle, w którym różne operacje produkcyjne są przekształcane z procesu ręcznego na proces zautomatyzowany lub zmechanizowany. [2] Automatyzacja nie dotyczy wyłącznie przemysłu. Z układów automatyki o różnym stopniu zaawansowania korzystamy na co dzień. Przykładem może tutaj być elektryczny czajnik, który wyłącza grzałkę po osiągnięciu przez wodę określonej temperatury, dzięki bimetalicznemu stycznikowi. Innym już bardziej zaawansowanym układem jest samochód, w którym proces sterowania dawką paliwa odbywa się automatycznie, uwzględniając wiele zmiennych, także zależnych od nas (żądana prędkość jazdy).
Słowo automatyka zostało ukute w połowie lat 40-tych XX wieku przez amerykański przemysł samochodowy w celu określenia automatycznego przenoszenia części pomiędzy maszynami produkcyjnymi. Pochodzi ono od greckiego słowa "automatos", oznaczającego samoczynne działanie. Postęp w dziedzinie komputerów i systemów sterowania rozszerzył definicję automatyzacji. Obecnie słownik języka polskiego definiuje to pojęcie jako „dział nauki i techniki zajmujący się urządzeniami sterującymi procesami technologicznymi bez udziału człowieka”. Automatyzacja istniała już od wielu lat na małą skalę i wykorzystywała urządzenia mechaniczne do zautomatyzowania produkcji przedmiotów o prostym kształcie. Jednak jej zastosowanie upowszechniło się dopiero wraz z pojawieniem się komputera, którego elastyczność pozwoliła na sterowanie niemal każdym rodzajem zadań. [2]
Robotyka to sztuka, baza wiedzy z wielu dziedzin i know-how projektowania, stosowania i wykorzystywania robotów w ludzkich przedsięwzięciach. Roboty w pojedynkę rzadko kiedy są użyteczne i dlatego stosuje się je razem z innymi urządzeniami i maszynami produkcyjnymi. Zazwyczaj są one zintegrowane w system, który jako całość ma za zadanie wykonać określone czynności. Systemy robotyczne składają się nie tylko z robotów, ale także z innych urządzeń i systemów, które są używane razem z robotami do wykonywania niezbędnych zadań. [2]
Słowo robot zawsze odnosi się do zautomatyzowanego wielofunkcyjnego manipulatora, który działa za pomocą energii, aby wykonywać różne zadania. Słowo robot zostało wprowadzone w 1920 roku w sztuce czeskiego pisarza Karela Capka pod tytułem R.U.R., czyli Uniwersalne Roboty Rossuma. Stąd też słowo robot pochodzi od czeskiego słowa robota, oznaczającego pracę przymusową lub znojną. W sztuce tej człekopodobne mechaniczne istoty produkowane w fabryce Rossuma są potulnymi niewolnikami. Ponieważ są tylko maszynami, są one źle traktowane przez ludzi. Pewnego dnia pewien niefrasobliwy naukowiec obdarza je emocjami, a roboty buntują się i zabijają prawie wszystkich ludzi, przejmując władzę nad światem. Jednak, ponieważ nie są one w stanie się rozmnażać, roboty są skazane na śmierć. Jednak jedyny ocalały człowiek tworzy męskiego i żeńskiego robota, aby mogły one przedłużyć ciągłość swojego gatunku. [2] Obecnie termin robot definiowany jest jako "urządzenie zastępujące człowieka przy wykonywaniu niektórych czynności", zaś robotyka jako "nauka zajmująca się projektowaniem i zastosowaniem robotów".
Jednym z pierwszych typów robotów był mechanizm kontrolny ze sprzężeniem zwrotnym (samokorygujący). Było to koryto do podlewania, które wykorzystywało pływak do wykrywania poziomu wody. Kiedy wody jest zbyt mało, pływak opada, otwiera zawór i więcej wody wpada do koryta. W miarę jak woda się podnosi, podnosi się również pływak. Gdy osiągnie określoną wysokość, zawór zostaje zamknięty i woda zostaje odcięta. W 1954 r. amerykański wynalazca George Devol, Jr. opracował prymitywne ramię, które można zaprogramować do wykonywania określonych zadań. W 1975 r. amerykański inżynier mechanik Victor Scheinman opracował wielofunkcyjny manipulator, znany jako programowalne uniwersalne ramię manipulacyjne (PUMA). PUMA była w stanie przemieszczać obiekt i umieszczać go w dowolnej orientacji w żądanym miejscu. Obecnie możliwości robotów wciąż są rozszerzane i doskonalone. W 1995 r. na świecie działało około 700 000 robotów. Jednym z głównych użytkowników robotów jest przemysł samochodowy.
Omówione dalej tematy są pewnymi fragmentami rozległej dziedziny wiedzy, które są niezbędne podczas opracowywania nowych urządzeń i układów regulacji. Starałem się tutaj dla odmiany od literatury związanej z tą tematyką wyjaśnić różne pojęcia w możliwie najprostszy i przejrzysty sposób.
Wyznaczanie modeli wybranych obiektów
Transformacja Laplace'a
Analiza częstotliwościowa wybranych modeli transmitancyjnych
Analiza czasowa wybranych modeli transmitancyjnych
Przekształcanie schematów blokowych
Wyznaczanie modeli wybranych obiektów
Aby zrozumieć i kontrolować złożone systemy, należy najpierw uzyskać ich ilościowe modele matematyczne. Konieczne jest więc przeanalizowanie zależności między zmiennymi systemu i uzyskanie modelu matematycznego. W praktyce złożoność układów i nasza niewiedza o wszystkich istotnych czynnikach wymuszają wprowadzenie założeń dotyczących jego działania. Dlatego często przydatne będzie rozważenie układu fizycznego, przyjęcie określonych założeń i linearyzacja układu. Jeżeli dynamika układu fizycznego może zostać opisana jednym, bądź wieloma równaniami różniczkowymi, to mówi się wtedy o jego reprezentacji za pomocą modelu matematycznego. Oczywiście równania te nie muszą być wyłącznie różniczkowe, jednak z uwagi na to, że rozpatrywane są obiekty dynamiczne, to zazwyczaj są to równania różniczkowe. Równania opisujące obiekt biorą się z podstawowych praw fizyki, a do ich zapisania wykorzystuje się np. formalizm d'Alamberta lub Lagrange'a w przypadku układów mechanicznych lub metodę prądów oczkowych dla układów elektrycznych. Następnie, wykorzystując narzędzia matematyczne, takie jak transformata Laplace'a, otrzymujemy rozwiązanie opisujące działanie układu. Podsumowując, podejście do modelowania układów dynamicznych można wymienić następujące: [3]
1. Zdefiniowanie systemu i jego elementów.
2. Sformułowanie modelu matematycznego i podstawowych założeń opartych na podstawowych zasadach fizyki.
3. Uzyskać równania różniczkowe reprezentujące model matematyczny.
4. Rozwiązać równania dla pożądanych zmiennych wyjściowych.
5. Zbadać rozwiązania i założenia.
6. W razie potrzeby ponownie przeanalizować lub przeprojektować system.
Na początek rozpatrzmy elementarny 1-masowy układ mechaniczny i spróbujmy zapisać dla niego równania, czyli dokonać jego reprezentacji za pomocą modelu matematycznego. Jest to o tyle niezbędne, ponieważ kolejne analizy i badania dynamiki takiego układu wymagają modelu matematycznego. Bez niego właściwie miemożliwe byłoby stwierdzenie o jego działaniu. Nawet jeżeli zostałby zbudowany układ, to nadal pozostaje pytanie, jakie wartości powinny mieć poszczególne jego elementy. Niewłasciwy ich dobór może spowodować, że będzie on sachowywał się niewłaściwie przy okreslonych oddziaływaniach zewnętrznych. Poza tym budowanie czegokolwiek bez przeprowadzenia wcześniejszych choćby podstawowych obliczeń nie jest podejściem inżynierskim.
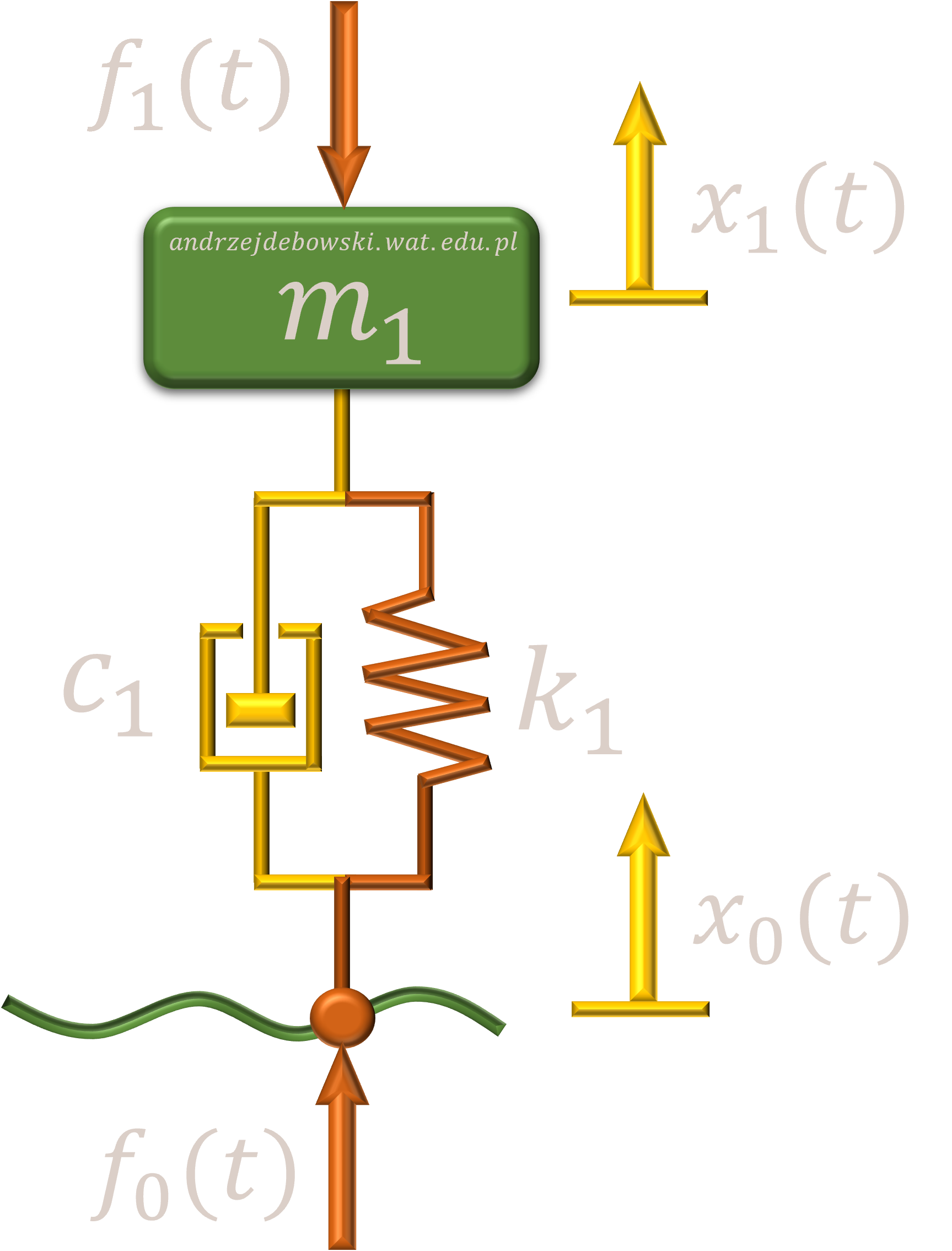
Rysunek przedstawia model, który może być reprezentacją samochodowego zawieszenia. W takim przypadku zakłada się, że koło jest bezmasowe, a masa m1 stanowi 1/4 całej masy pojazdu. Pomija się efekty związane z tarciem suchym oraz wszystkie efekty związane z tłumieniem materiałowym w sprężynie k1. Wartość parametru c1 jest tłumieniem wiskotycznym amortyzatora. Układ posiada także możliwość oddziaływania zewnętrzną siłą f1(t) oraz pobudzeniem kinematycznym f0(t) imitującym profil jezdni. Odpowiedzią układu na oba te pobudzenia będzie przemieszczenie x1 masy m1.
Teraz zastanówmy się skąd wezmą się równania opisujące dynamikę takiego układu. Możliwości zapisu tych równań jest wiele, jednak większość jest zbyt skomplikowana, aby stosować je do tak prostego zagadnienia. Mowa tutaj np. o równaniach Lagrange'a lub Hamiltona. Zazwyczaj bywa tak, że wykorzystuje się określony sposób wyprowadzania równań do określonych struktur układów. W tym przypadku wystarczająca będzie zasada d'Alamberta. Analizuje się wtedy siły powstające pomiędzy poszczególnymi elementami układu w równowadze statycznej. W ten sposób otrzymujemy równoważny schemat widoczny poniżej. Warto zaznaczyć, że skoro układ jest w równowadze statycznej, to pomija się przy tym siłę ciężkości lub mówiąc ściślej podczas rozważań redukuje się ona.
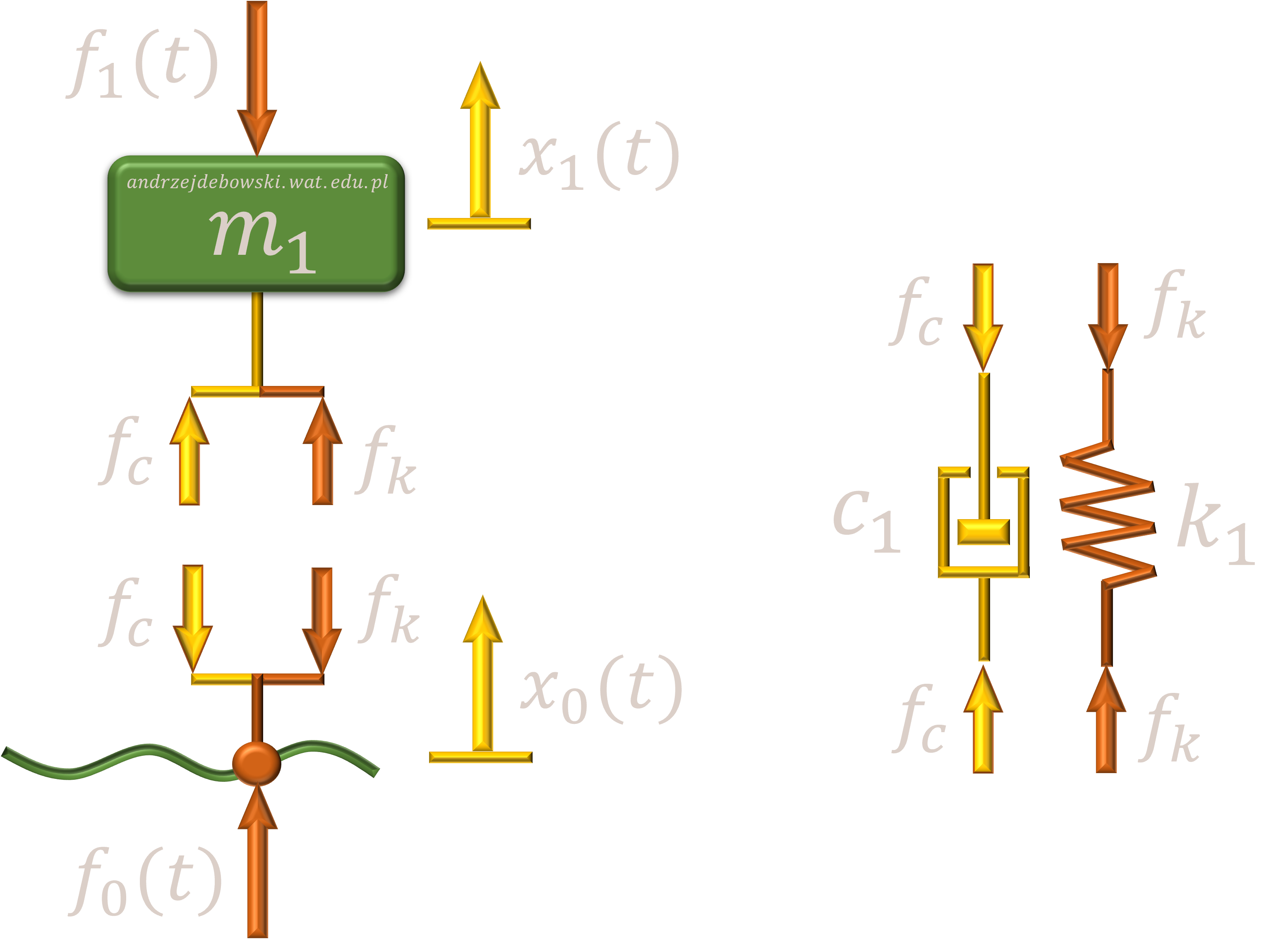
Na podstawie takiego schematu można zapisać następujące równania:
$$m_1 \ddot{x}_1(t)+f_c+f_k=f_1(t)$$
$$f_0(t)=f_c+f_k$$
$$f_k=k_1\big(x_1(t)-x_0(t)\big)$$
Siła fc wynika z siły tłumienia amortyzatora, która związana jest z prędkością.
$$f_c=c_1 \big(\dot{x}_1(t)-\dot{x}_0(t)\big)$$
Siła fk wynika z siły sprężystości przy uginaniu sprężyny, która związana jest z przemieszczeniem.
$$f_k=k_1\big(x_1(t)-x_0(t)\big)$$
Po podstawieniu oraz uporządkowaniu otrzymuje się ostatecznie:
$$m_1\ddot{x}_1(t)+c_1 \big(\dot{x}_1(t)-\dot{x}_0(t) \big)+k_1 \big({x}_1(t)-{x}_0(t) \big)=f_1(t)$$
Mając już model matematyczny obiektu można przejść do następnego kroku, czyli analiz. Model ten jest w dziedzinie czasu, więc na tym etapie analizy mogą odbywać się wyłącznie poprzez rozwiązanie równania różniczkowego. Ze względu na powszechność oprogramować wspomagających obliczenia zostanie ten model przeniesiony do środowiska LabVIEW. W środowisku tym możliwe jest rozwiązanie równania w sposób iteracyjny, czyli wartości obliczone, są w kolejnym kroku wartościami wejściowymi, a obliczenia trwają tyle ile założy sobie badacz, aby obliczenia się wykonały. Jednak aby to zrobić niezbędne jest przekształcenie równania do postaci użytecznej w LabVIEW, czyli należy wyznaczyć najwyższą pochodną z równania. Wtedy równanie przyjmie następującą postać:
$$ \ddot{x}_1(t)=\frac{-c_1 \big(\dot{x}_1(t)-\dot{x}_0(t) \big)-k_1 \big({x}_1(t)-{x}_0(t) \big)+f_1(t)}{m_1} $$
Jednak z uwagi na to, że rozpatrujemy dynamikę układu na Ziemi, to ostatecznie występuje siła ciężkości g i nie należy jej pomijać. Trzeba jednak pamiętać o zachowaniu konwencji znaków, aby oddziaływanie tej siły miało właściwy skutek. Siła ciężkości ma także jeszcze jedno praktyczne zastosowanie. Umożliwia wykonanie elementarnego testu modelu komputerowego. Jeżeli początkowa wartość była równa 0, to po wprowadzeniu 9,81 m/s2, położenie masy m1 powinno ulec zmianie. W tym przypadku wartość przemieszczenia powinna się zmniejszyć.
$$\ddot{x}_1(t)=\frac{m_1 \cdot g -c_1 \big(\dot{x}_1(t)-\dot{x}_0(t) \big)-k_1 \big({x}_1(t)-{x}_0(t) \big)+f_1(t)}{m_1}$$
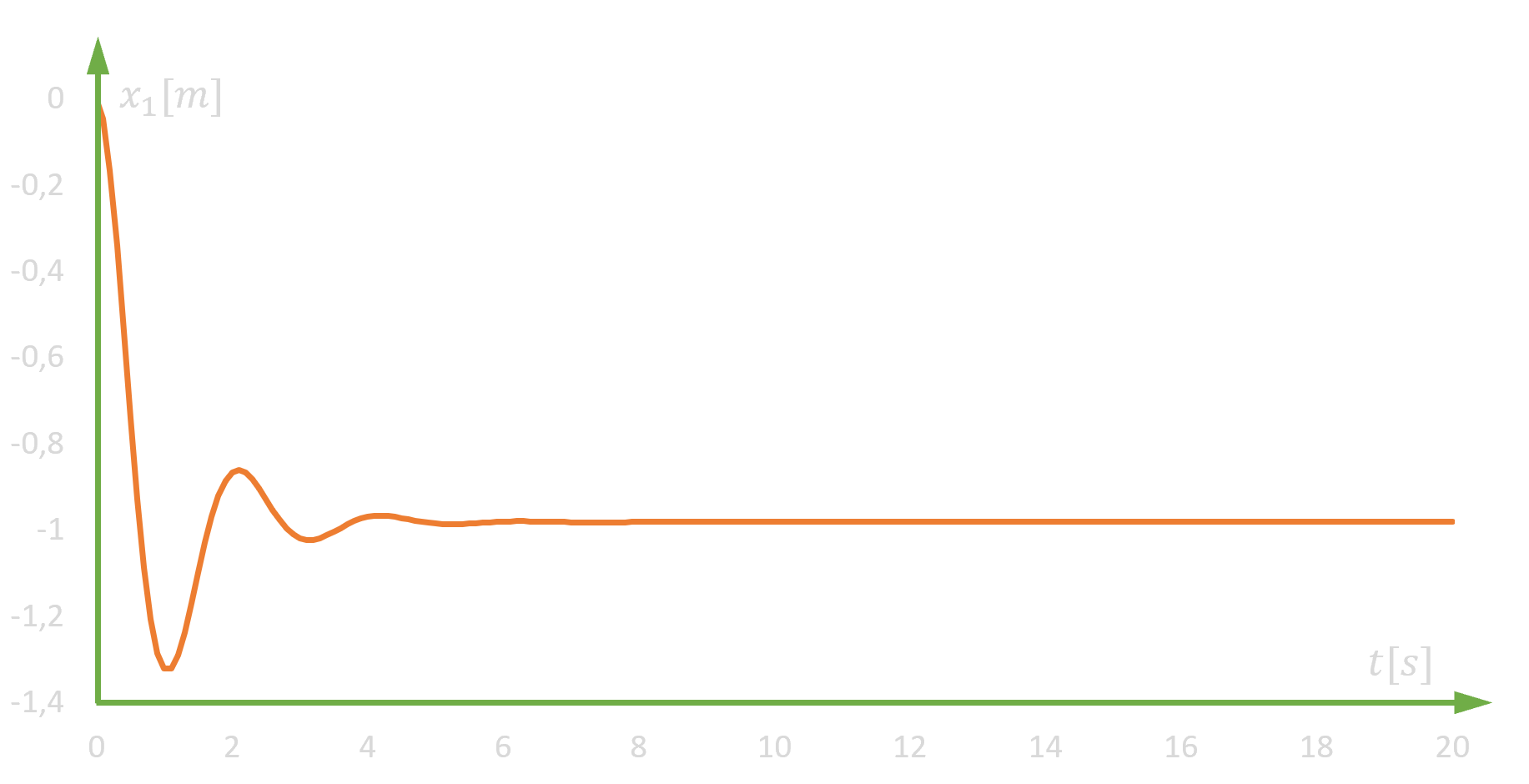
Otrzymany model matematyczny jest w postaci parametrycznej. Jeżeli teraz przyjmiemy określone wartości parametrów modelu i użyjemy odpowiedniego oprogramowania, to możemy Otrzymać wykres widocznY poniżej. Wartości parametrów modelu są następujące: m1=0,5 kg, c1=1 Ns/m, k1=5 N/m. Jest to symulacja ruchu masy m1 przy f0=0 oraz f1=0 i od warunków początkowych równych 0.
W przypadku chęci obserwacji zachowania układu pod wpływem siły f0 lub f1, niezbędne jest wydłużenie czasu obliczeń, gdyż w pierwszej kolejności model musi znajdować się w równowadze. Inaczej ocena oddziaływania danej siły na układ będzie nie tylko trudna, co wręcz bezcelowa. Na podstawie pierwszego badania można stwierdzić, że układ osiąga równowagę w około 6 sekundzie. W związku z tym oddziaływanie siły f0 lub f1 można dla pewności rozpocząć od 10 sekundy. Przy oddziaływaniu siłą f1 o charakterze sinusoidalnym układ zachowuje się tak, jak na poniższym wykresie.
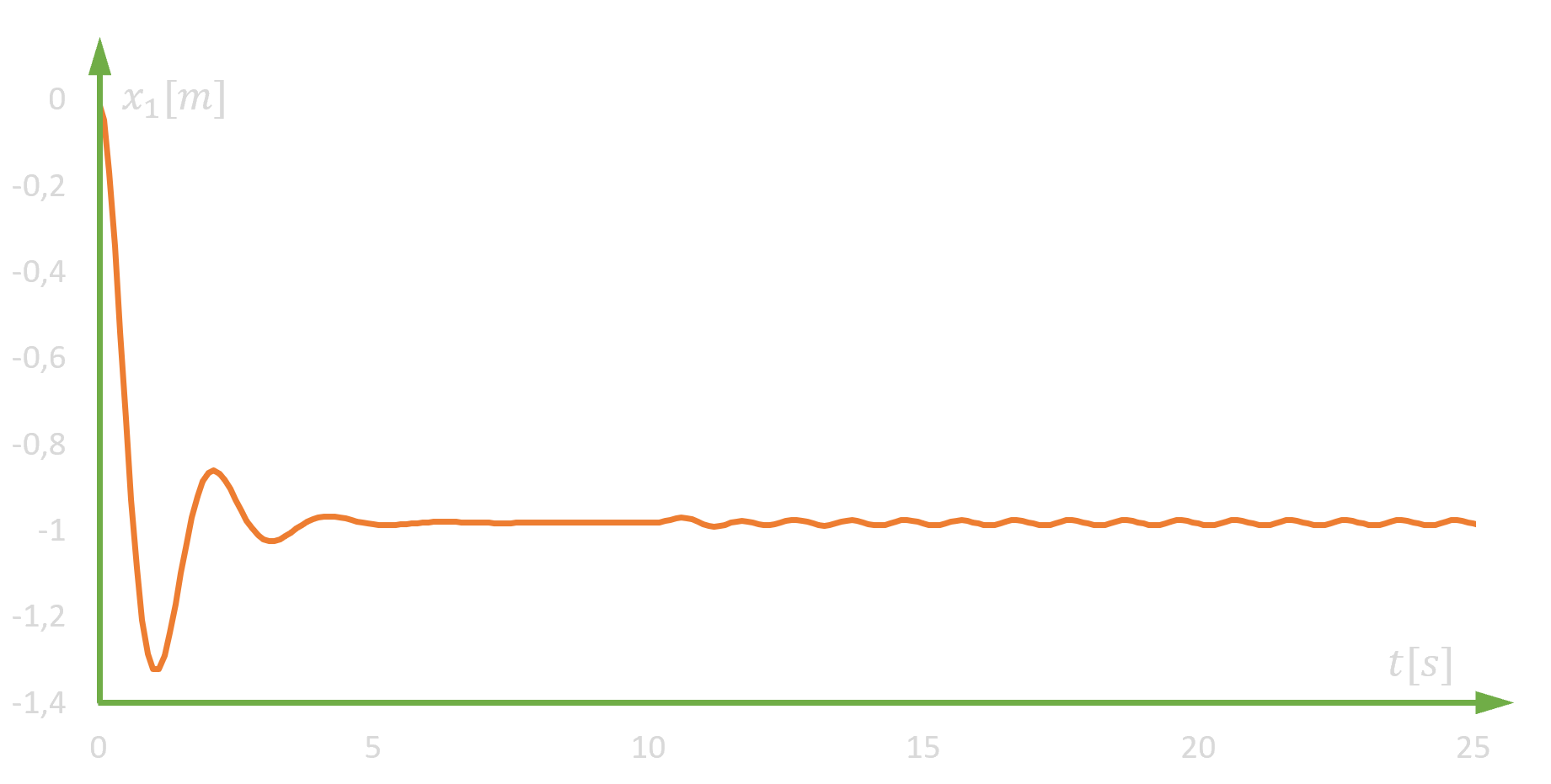
W przypadku oddziaływania siłą f0 zachowanie układu obrazuje poniższy wykres.
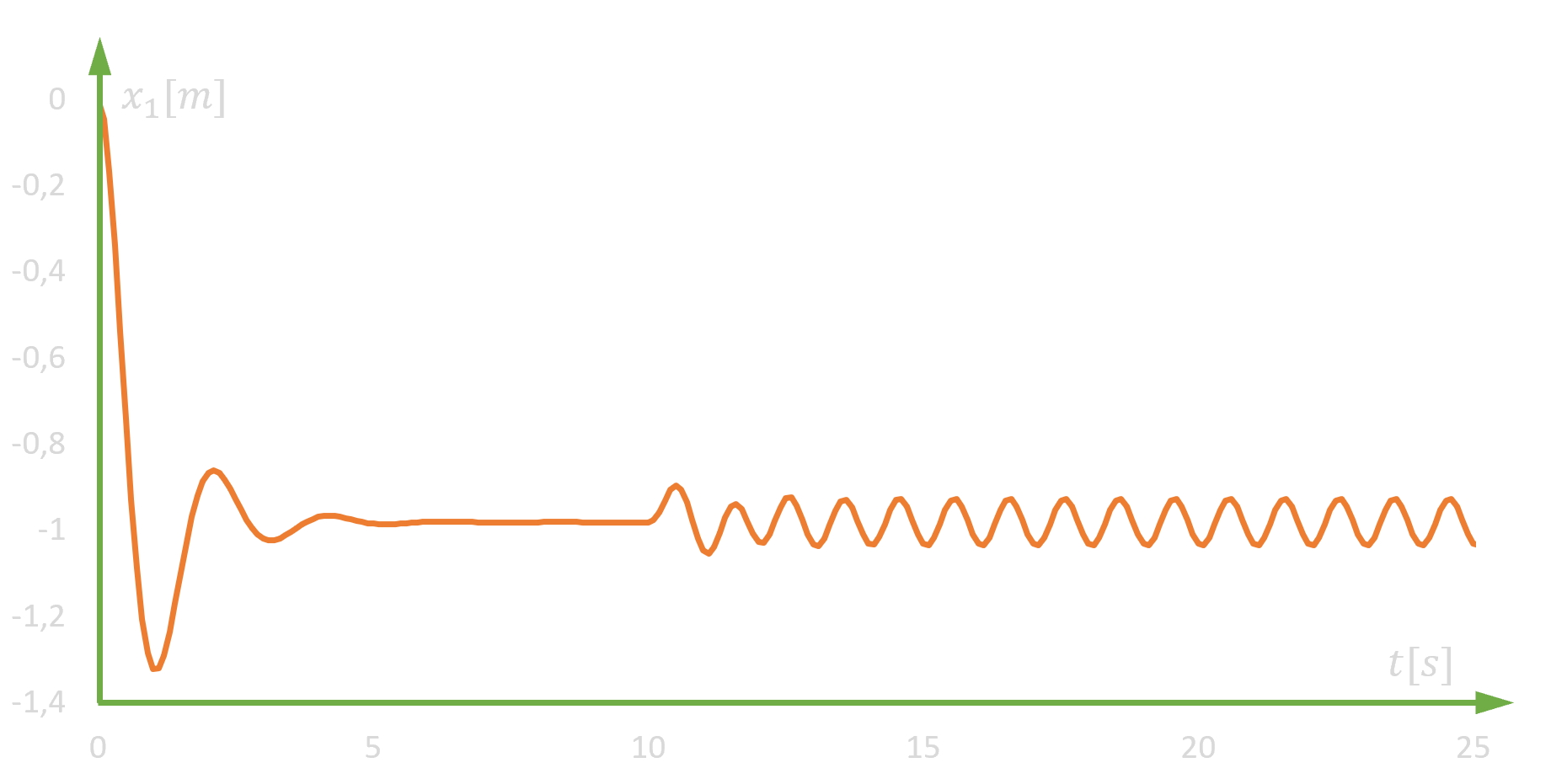
Już na podstawie tak prostego układu możemy dzięki symulacji dostrzec bardzo ciekawe jego zachowanie. Otóż w obydwu przypadkach sygnałem pobudzenia był przebieg sinusoidalny o jednakowej częstotliwości (0,5 Hz) i amplitudzie (0,1 m), jednak odpowiedź układu na identyczne wymuszenie jest inna w zależności od miejsca przyłożenia oddziaływania. Niestety w przypadku analizy czasowej trudno jest ustalić przyczyny takiego zachowania badanego obiektu. I tu z pomocą przychodzi analiza częstotliwościowa.
Transformacja Laplace'a
Jednostronne dodatnio określone całkowe przekształcenie Laplace'a, które będziemy określać krótko transformacją Laplace'a zapisuje się następująco:
$$F(s)=\mathcal{L}[f(t)]=\int\limits_{0+}^{+\infty} e^{-st} f(t)dt$$
Pozwala ono na przejście z dziedziny czasu t do dziedziny operatora s. Co to dla nas oznacza? Oznacza przede wszystkim, że zamiast f(t) będziemy teraz pisali F(s). Natomiast od strony praktycznej przekształcenie to pozwala rozwiązać różne zagadnienia w prostszy sposób, co wynika z własności transformaty. Własności te powodują, że na płaszczyźnie zespolonej mnożenie funkcji przez s daje efekt różniczkowania, a dzielenie całkowania. Może się to wdawać na tym etapie dość niejasne, ale w praktycznych zastosowaniach jest to niezwykle pomocne. W związku z tym transformację Laplace'a można wykorzystywać zarówno do wyznaczenia rozwiązywania równań różniczkowych, jak i transmitancji. Należy jednak pamiętać, że w przypadku transmitancji warunki początkowe muszą być równe zero. W praktyce rzadko konieczne jest skorzystanie z powyższego wzoru, gdyż duża liczba najczęściej stosowanych transformat znajduje się w tablicach. Najczęściej stosowane funkcje zestawiono w tabeli 1, zaś więcej można znaleźć tu: Transformaty Laplace'a.
$$Numer$$ |
$$Funkcja oryginału$$ |
$$Transformata Laplace'a$$ |
| 1. | $$f(t)$$ |
$$\mathcal{L}[f(t)]=\int\limits_{0+}^{+\infty} e^{-st} f(t)dt$$ |
| 2. | $$f(t)$$ |
$$F(s)$$ |
| 3. | $${f'}(t)$$ |
$$sF(s)-f(0+)$$ |
| 4. | $${f''}(t)$$ |
$$s^2F(s)-sf(0+)-f'(0+)$$ |
| 5. | $${f'''}(t)$$ |
$$s^3F(s)-s^2f(0+)-sf'(0+)-f''(0+)$$ |
| 6. | $${f''''}(t)$$ |
$$s^4F(s)-s^3f(0+)-s^2f'(0+)-sf''(0+)-f'''(0+)$$ |
| 7. | $$f^n(t)$$ |
$$s^nF(s)-s^{n-1}f(0+)-s^{n-2}f'(0+)-...--f^{n-1}(0+)$$ |
| 8. | $$\int f(t)$$ |
$$\frac{1}{s}F(s)$$ |
| 9. | $$\int\int f(t)$$ |
$$\frac{1}{s^2}F(s)$$ |
| 10. | $$a \cdot 1(t)$$ |
$$a \cdot \frac{1}{s}$$ |
| 11. | $$\delta (t)$$ |
$$1$$ |
| 12. | $$\delta '(t)$$ |
$$s$$ |
| 13. | $$a sin(\omega t)$$ |
$$\frac{a\omega}{s^2+\omega^2}$$ |
| 14. | $$a cos(\omega t)$$ |
$$\frac{as}{s^2+\omega^2}$$ |
| 15. | $$e^{at}$$ |
$$\frac{1}{(s-a)}$$ |
| 16. | $$e^{-at}$$ |
$$\frac{1}{(s+a)}$$ |
| 17. | $$te^{at}$$ |
$$\frac{1}{(s-a)^2}$$ |
| 18. | $$\frac{1}{b}e^{\frac{at}{b}}$$ |
$$\frac{1}{bs-a}$$ |
| 19. | $$\frac{1}{b}e^{-\frac{at}{b}}$$ |
$$\frac{1}{bs+a}$$ |
| 20. | $$a \cdot t$$ |
$$\frac{a}{s^2}$$ |
| 21. | $$a \cdot t^2$$ |
$$\frac{2a}{s^3}$$ |
Mając już równanie opisujące 1-masowy układ, czyli model matematyczny jest następujące:
$$ m_1\ddot{x}(t)+c_1 \big(\dot{x}_1(t)-\dot{x}_0(t) \big)+k_1 \big({x}_1(t)-{x}_0(t) \big)=f_1(t)-m_1 \cdot g $$
Powyższe równanie może być zapisane także z pominięciem dziedziny czasu czyli:
$$ m_1\ddot{x}+c_1 \big(\dot{x}_1-\dot{x}_0 \big)+k_1 \big({x}_1-{x}_0 \big)=f_1-m_1 \cdot g $$
lub też stosując notację Leibniza:
$$ m_1 \frac{d^2x_1}{dt^2}+c_1 \left(\frac{dx_1}{dt}-\frac{dx_0}{dt} \right)+k_1(x_1-x_0)=f_1-m_1 \cdot g $$
Podsumowując powyższe mamy jedno równanie, w którym z masą m1 związane jest przyspieszenie, z tłumieniem c1 prędkość, a ze sztywnością k1 przemieszczenie. Jeżeli mas byłoby więcej, to również liczba równań będzie większa. W rozpatrywanym przypadku te trzy parametry są niezależne od czasu, czyli wraz z jego upływem ich wartość się nie zmieni. Natomiast już f1(t), f0(t), x1(t) oraz x0(t), mogą się zmieniać, gdyż zależą one od czasu. Rozpatrując te zmienne zgodnie z definicją transmitancji operatorowej zmienne f1(t) i f0(t) będą zatem wymuszeniem czyli wejściem i mogą one być dowolną funkcją lub też jednorazowym impulsem. Decyzja o tym należy do badacza. Natomiast x1(t) będzie odpowiedzią układu czyli wyjściem. W przypadku funkcji x0(t) także jest ona sygnałem wymuszenia, gdyż jest bezpośrednio związana z f0(t) i stanowi niejako informację o przebiegu wymuszenia.
Przejdźmy do wyznaczenia transmitancji układu. Stosując transformację Laplace'a możemy zapisać to równanie w innej postaci. Nadal będzie to model matematyczny opisujący ten obiekt, jednak odnosić się będzie do innej dziedziny oraz będzie można wykonać innego rodzaju analizy. Model można teraz zapisć w postaci transmitancji operatorowej G(s). Do tego jest potrzebna albo umiejętność stosowania całki Laplace'a, albo posiadanie tabeli transformat.
Zgodnie z tabelą 1 (wzór 2) można napisać, że:
$$ \mathcal{L}[f_1(t)]=F_1(s), \mathcal{L}[f_0(t)]=F_0(s), \mathcal{L}[x_1(t)]=X_1(s), \mathcal{L}[x_0(t)]=X_0(s). $$
Powyższy zapis może wydawać się zbędny, ale konieczne jest rozróżnienie w zapisie funkcji zależnej od czasu od tej w dziedzinie operatorowej.
Następnie stosując dodatkowo wzór 3 i 4 z tabeli 1 otrzymamy następujące równanie już w dziedzinie operatorowej, zapisane poniżej. Warto zauważyć, że transformata funkcji we wzorach 3 i 4 ma dodatkowe składniki, które są odejmowane, są to warunki początkowe. W przypadku wyznaczania transmitancji pomija się tę elementy, co wynika z definicji transmitancji.
$$ m_1s^2X_1(s)+c_1 \big(sX_1(s)-sX_0(s)\big)+k_1 \big(X_1(s)-X_0(s)\big)=F_1(s)-m_1 \cdot g $$
Można tutaj zauważyć bezsprzeczną zaletę transformacji Laplace'a. Otóż z równania różniczkowego otrzymaliśmy równanie algebraiczne. Dzięki temu dalsze przekształcenia stają się o wiele prostsze. Z uwagi na to, że układ ma dwa wejścia i jedno wyjście, to możemy zapisać dwie transmitancje o postaci:
$$ G_1(s)=\frac{X_1(s)}{F_1(s)}, G_2(s)=\frac{X_1(s)}{X_0(s)}$$
Teraz pozostaje wykonać kilka przekształceń, gdzie w pierwszym wyłączamy wspólny czynnik przed nawias, a pozostałe elementy przenosimy na prawą stronę oraz zastosujemy podstawienie:
$$F_2(s)=F_1(s)-m_1 \cdot g $$
Jest ono niezbędne, gdyż inaczej siła ciężokści uniemożliwi zapisanie transmitancji. W związku z powyższym otrzymujemy:
$$ X_1(s) \cdot (m_1s^2+c_1s+k_1)=X_0(s) \cdot (c_1s+k_1)+F_2(s)$$
Ostatecznie otrzymuje się dwie transmitancje, gdzie pierwsza G1 ma postać:
$$ \frac{X_1(s)}{F_2(s)}=\frac{1}{m_1 \cdot s^2+c_1 \cdot s+k_1} $$
zaś druga G2:
$$ \frac{X_1(s)}{X_0(s)}=\frac{c_1 \cdot s+k_1}{m_1 \cdot s^2+c_1 \cdot s+k_1} $$
Analiza częstotliwościowa wybranych modeli
Mając transmitancje opisujące zachowanie układu można narysować jeden z wykresów częstotliwościowych. Do najpopularniejszych należą wykresy Bode'go i Nyquista. Jednak wykorzystywane mogą być także wykresy Black'a, charakterystyka składowej części rzeczywistej i urojonej transmitancji lub modułu i fazy transmitancji w postaci liniowej. Jednak przedstawione tutaj zostaną dwa pierwsze.
Aby wyznaczyć poszczególne wykresy należy najpierw dokonać podstawienia s=jω, otrzymując w ten sposób transmitancję widmową widoczną poniżej.
$$ G_1(j\omega)=\frac{X_1(j\omega)}{X_0(j\omega)}=\frac{c_1 \cdot j\omega+k_1}{m_1 \cdot j^2\omega^2+c_1 \cdot j\omega+k_1} $$
Mając na uwadze własności liczby urojone, w tym przypadku wystarczy pamiętać, że j podniesione do kwadratu jest równe -1, to transmitancja widmowa G2(jω) będzie następująca:
$$ \frac{X_1(j\omega)}{X_0(j\omega)}=\frac{c_1 \cdot j\omega+k_1}{-m_1 \cdot \omega^2+c_1 \cdot j\omega+k_1} $$
Teraz niezbędne jest wyznaczenie części rzeczywistej i urojonej transmitancji widmowej. Można toego dokonać poprzez pomnożenie transmitancji o liczbę sprzężoną. Należy jednak zwrócić uwagę, na sposób jej tworzenia. Mianowicie liczby urojone zmieniają znak, a rzeczywiste nie. Czyli kolejne wyrażenie przyjmie postać:
$$ \frac{X_1(j\omega)}{X_0(j\omega)}=\frac{c_1 \cdot j\omega+k_1}{-m_1 \cdot \omega^2+c_1 \cdot j\omega+k_1} \cdot \frac{-m_1 \cdot \omega^2-c_1 \cdot j\omega+k_1} {-m_1 \cdot \omega^2-c_1 \cdot j\omega+k_1} $$
Po wymnożeniu i uporządkowaniu otrzymuje się:
$$ \frac{X_1(j\omega)}{X_0(j\omega)}=\frac{c_1^2\omega^2-k_1\omega^2m_1-jc_1\omega^2m_1+k_1^2}{m_1^2\omega^4-2k_1m_1\omega^2+c_1^2\omega^2 +k_1^2} $$
Natomiast po rozdzieleniu części rzeczywistej i urojonej:
$$ \frac{X_1(j\omega)}{X_0(j\omega)}=\frac{c_1^2\omega^2-k_1\omega^2m_1+k_1^2}{m_1^2\omega^4-2k_1m_1\omega^2+c_1^2\omega^2 +k_1^2} - j\frac{c_1\omega^2m_1}{m_1^2\omega^4-2k_1m_1\omega^2+c_1^2\omega^2 +k_1^2}$$
Na podstawie powyższego można zapisać końcową postać części rzeczywistej i urojonej transmitancji widmowej, a mianowicie:
$$ P(\omega)=\frac{c_1^2\omega^2-k_1\omega^2m_1+k_1^2}{m_1^2\omega^4-2k_1m_1\omega^2+c_1^2\omega^2 +k_1^2} $$
$$ Q(\omega)=\frac{-c_1\omega^2m_1}{m_1^2\omega^4-2k_1m_1\omega^2+c_1^2\omega^2 +k_1^2}$$
Mając już P(ω) oraz Q(ω) w postaci parametrycznej można narysować wykres Nyquista. Wystarczy tylko za ω podstawić wybrane przez siebie wartości częstotliwości. Parametry modelu, podobnie jak poprzednio, mają: m1=0,5 kg, c1=1 Ns/m, k1=5 N/m. Kolejne wartosci P(ω) oraz Q(ω) zestawiono w tabeli 2.
$$\omega$$ |
0 |
2,0 |
2,5 |
2,9 |
3,2 |
3,7 |
4,5 |
6,0 |
50,0 |
$$P(\omega)$$ |
1,000 |
1,462 |
1,600 |
1,370 |
0,940 |
0,261 |
-0,116 |
-0,141 |
-0,002 |
$$Q(\omega)$$ |
0 |
-0,308 |
-0,800 |
-1,349 |
-1,598 |
-1,482 |
-0,979 |
-0,527 |
-0,040 |
Napotstawie tabeli 2 można sporządzić następujący wykres:
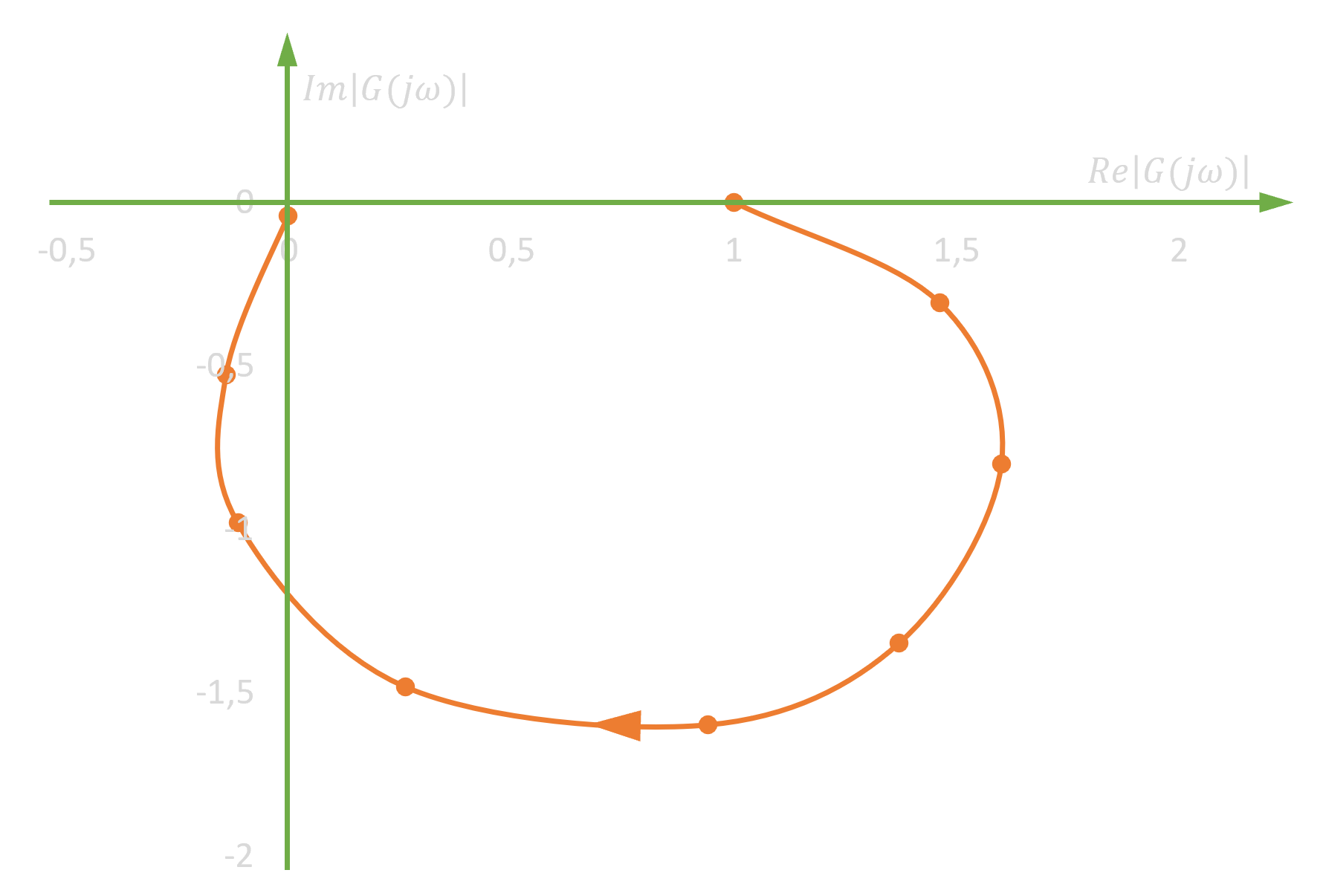 Im większa będzie liczba kolejnych wartości ω, tym dokładniejszy wykres się otrzyma, jednak w praktyce wystarczających jest tylko kilka.
Im większa będzie liczba kolejnych wartości ω, tym dokładniejszy wykres się otrzyma, jednak w praktyce wystarczających jest tylko kilka.
Analiza czasowa wybranych modeli
Charakterystyką czasową członu lub układu nazywamy przebieg jego wielkości wyjściowej, uzyskany pod wpływem impulsowej lub skokowej zmiany wielkości wejściowej, przy czym przed tą zmianą układ znajdował się w stanie ustalonym. Daje ona możliwość (w odniesieniu do układów jednowymiarowych) bezpośredniej oceny układu, ponieważ charakterystyka czasowa jest przebiegiem w czasie odpowiedzi y(t) układu dynamicznego na określone wymuszenie x(t).
Jako wymuszenie mogą być stosowane poniższe sygnały, jednak w kontekście badania układów najczęściej mówi się o odpowiedzi skokowej oraz impulsowej. Są one najczęściej wykorzystywane do oceny właściwości dynamicznych układów ciągłych.
$$ Nazwa$$ |
$$ f(t) $$ |
$$ F(s) $$ |
$$ Wykres $$ |
Skok jednostkowy - Funkcja Heaviside'a |
$$ 1(t) $$ |
$$ \frac{1}{s}$$ |
|
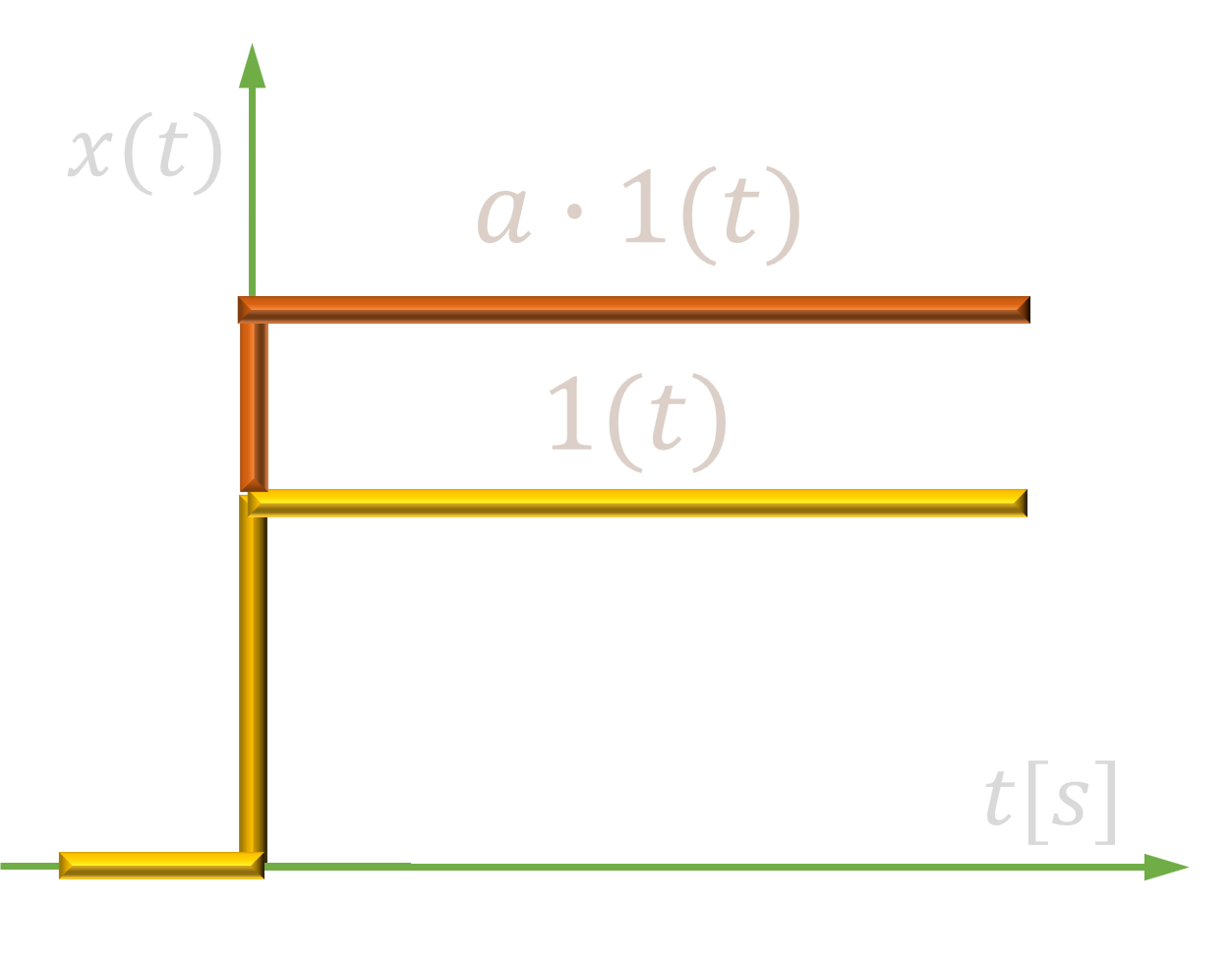
Wymuszenie skokowe |
$$ 1(t) \cdot a $$ |
$$ \frac{a}{s} $$ |
|
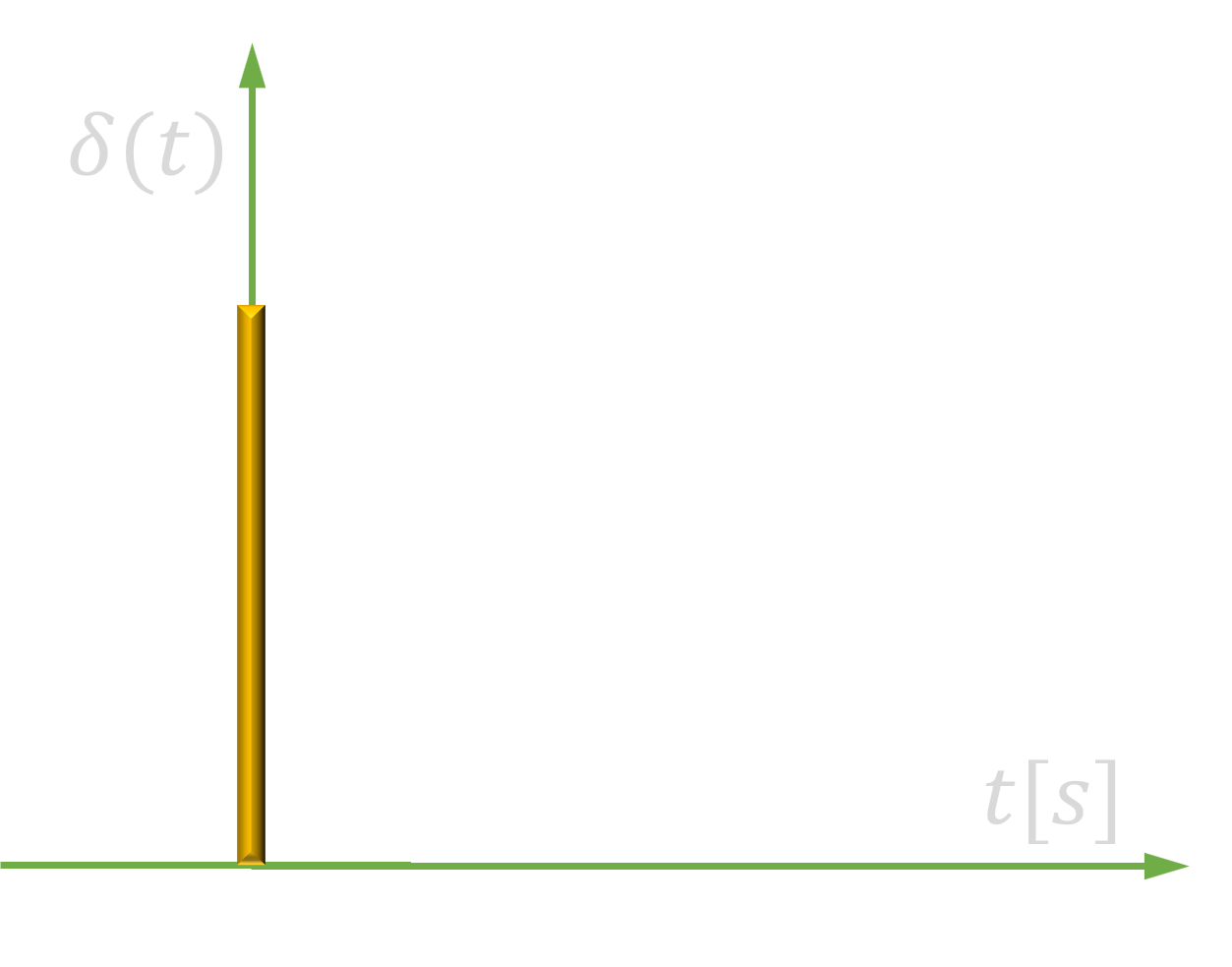
Wymuszenie impulsowe - Funkcja Diraca |
$$ a\cdot \delta(t) $$ |
$$ a \cdot 1$$ |
|
Wymuszenie liniowe |
$$ a\cdot t $$ |
$$ \frac{a}{s^2} $$ |
|
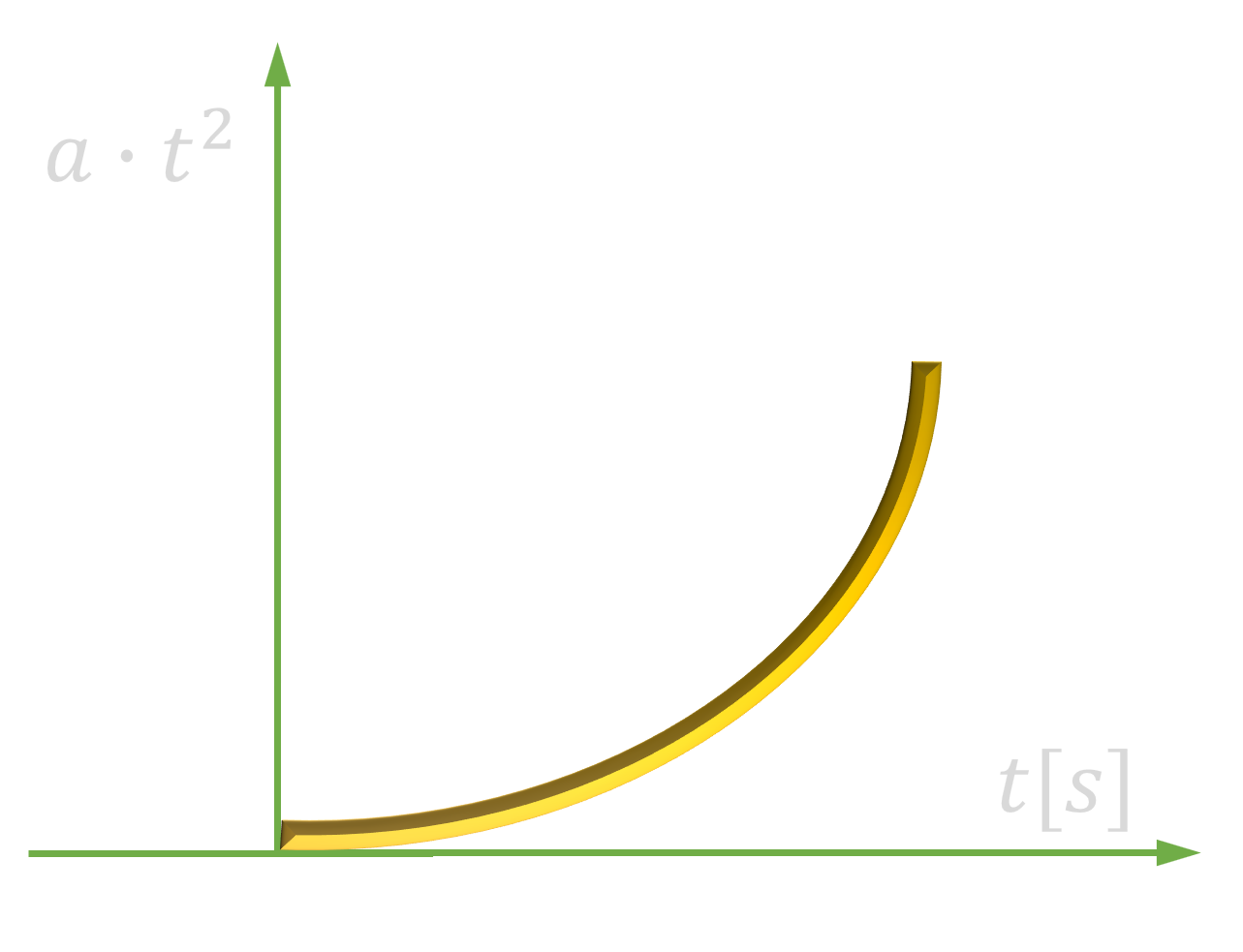
Wymuszenie paraboliczne |
$$ a \cdot t^2$$ |
$$ \frac{2a}{s^3}$$ |
Przekształcanie schematów blokowych
Do zobrazowania procesów zachodzących w obiekcie wykorzystuje się schemat technologiczny, na którym przedstawia się poszczególne urządzenia technologiczne i sposób ich połaczenia, stosując symbole oddające wygląd lub zasadę działania elementów. Schemat taki zawiera wiele szczegółów, które są istotne z punktu widzenia przygotowywanego projektu technicznego, jednak nie mają są użyteczne przy analizowaniu pracy obiektu na pewnym poziomie uogólnienia. Do celów badawczych wykorzystywane są schematy blokowe, które są uproszcznymi zobrazowaniami obiektu. Schematy blokowe (oraz grafy przepływu sygnałów) są bardzo wygodnymi i naturalnymi narzędziami do projektowania i analizy skomplikowanych układów sterowania. Schemat taki dostarcza informacji o powiązaniach pomiędzy blokami i sygnałami, zaś projektant może w łatwy sposób dodawać bloki do istniejącego schematu w celu poprawienia jakości sterowania. Poszczególne bloki mogą dodatkowo zawierać transmitancje opisujące poszczególne elementy układu, a poszczególne linie, węzły zaczepowe i sumacyjne pozwalają na zobrazowanie przepływu sygnałów w celu graficznego przedstawienia wzajemnych powiązań. [4] Schemat blokowy układu jest graficznym opisem funkcji wykonywanych przez każdy element rzeczywistego układu i przepływających między nimi sygnałów. W odróżnieniu od abstrakcyjnego opisu matematycznego, schematy blokowe mają tę zaletę, że bardziej realistycznie przedstawiają przepływy sygnałów w układzie. Tworzy się je bezpośrednio na podstawie układu równań opisujących schemat ideowy układu. Poszczególnym równaniom przyporządkowuje się elementy strukturalne schematu blokowego, które łączy się razem.
Modelowanie układów w postaci schematów blokowych realizuje się za pomocą trzech podstawowych elementów. Są to:
- bloki,
- węzły sumacyjne,
- węzły zaczepowe.
Blok
Na schematach blokowych wszystkie zmienne są powiązane ze sobą poprzez bloki funkcyjne. Bloki te są odpowiednikami operacji matematycznych wykonywanych na sygnałach wejściowych dając w odpowiedzi sygnały wyjściowe. Należy pamiętać, że bloki są elementami jednokierunkowymi, mającymi jedno wejście i jedno wyjście, w których znajdują się postacie transmitancyjne obiektów rzeczywistych. Zaletą schematu blokowego jest to, że łatwo jest uformować schemat blokowy dla całego układu poprzez połączenie bloków przepływającymi sygnałami i wówczas możliwa jest ocena wpływu każdego składnika na działanie całego układu. Poza tym zawiera on informacje o zachowaniu dynamicznym układu.
Węzeł sumacyjny
Pusty okrąg lub też okrąg z krzyżykiem na schematach blokowych oznacza operację algebraicznego sumowania sygnałów. Znak plus (może też nie być zaznaczony) lub minus przy każdej ze strzałek informuje o tym czy sygnał ten jest dodawany czy też odejmowany. Dla sygnałów, które mają być odejmowane musi być zawsze zaznaczony znak minus. Na schemacie blokowym węzeł sumacyjny może mieć wiele sygnałów wchodzących, ale tylko jeden wychodzący.
Węzeł rozgałęźny
Węzeł rozgałęźny jest punktem, z którego sygnał rozchodzi się do innych bloków lub węzłów sumacyjnych. Nie ma znaczenia w którym miejscu na danej linii się on znajduje oraz ile linii łączy. Czasami niektóre węzły umieszczane są dla zwiększenia przejrzystości schematu, co niekiedy może utrudniać jego przekształcanie.
Schematy blokowe przeważnie upraszcza się do postaci o mniejszej liczbie bloków przy użyciu algebry schematów blokowych. Schematy blokowe przedstawiają transformowane przy użyciu przekształceń Laplace'a równania układu, dlatego też przekształcanie układu jest równoważne algebraicznemu przekształcaniu równań. Dla schematów blokowych z pojedynczym wejściem i wyjściem, redukcja oznacza upraszczanie schematu do postaci, w której pozostanie już tylko pojedynczy blok zawierający transmitancję zastępczą znajdującą się pomiędzy wejściem i wyjściem. W redukcji schematów blokowych, bardzo pomocne jest prowadzenie jej krok po kroku, zawsze utrzymując tą samą zależność pomiędzy wejściem i wyjściem.
Numer |
Nazwa operacji |
Schemat wyjściowy |
Schemat równoważny |
| 1. | Połączenie szeregowe |  |
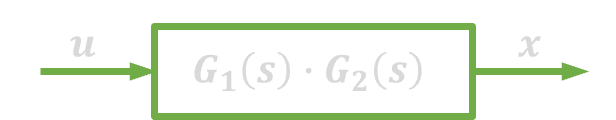 |
| 2. | Zamiana kolejności członów |  |
 |
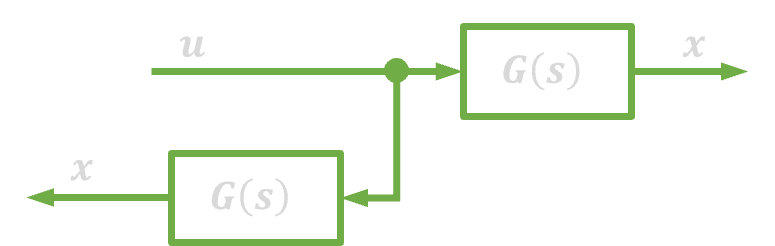
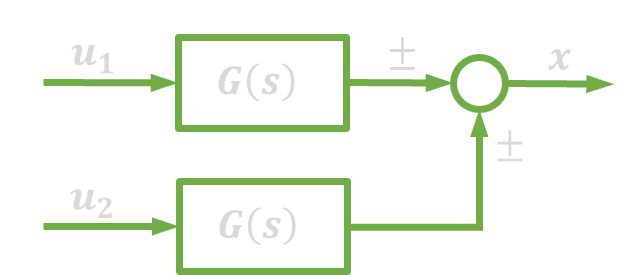
| 3. | Połączenie równoległe | 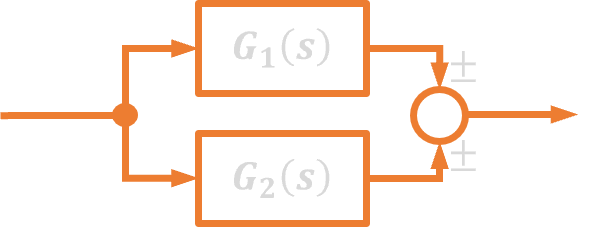 |
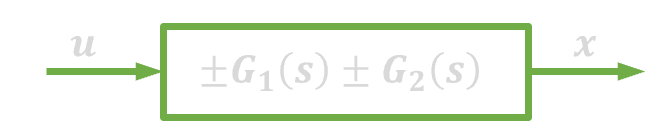 |
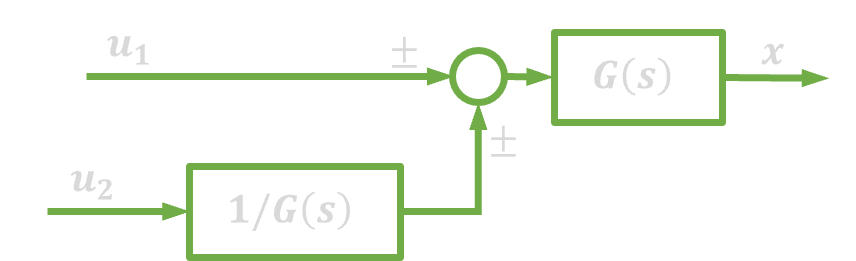
| 4. | Sprzężenie zwrotne | 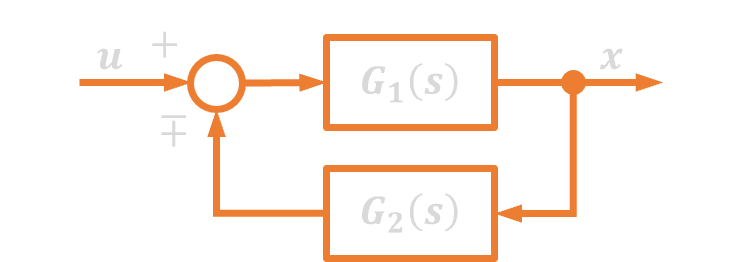 |
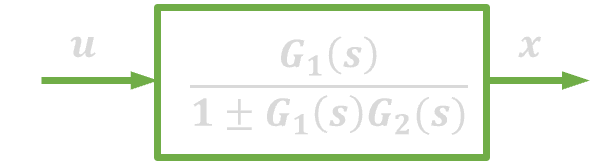 |
| 5. | Przesuwanie węzła zaczepowego za blok | 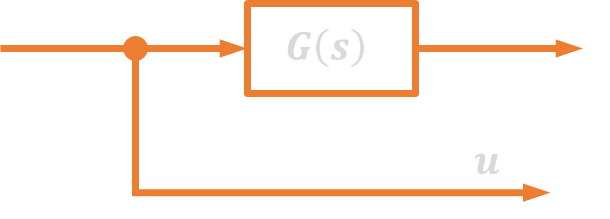 |
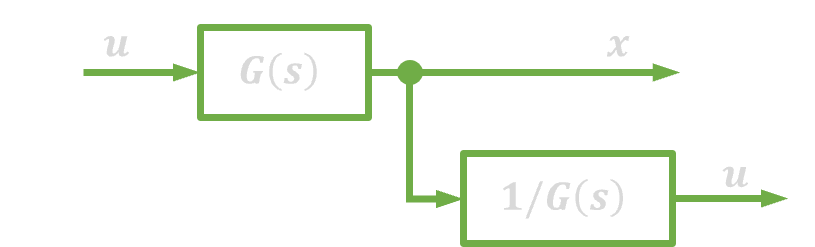 |
| 6. | Przesuwanie węzła zaczepowego przed blok | 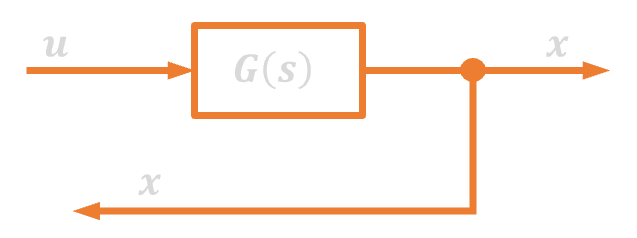 |
 |
| 7. | Przesuwanie węzła sumacyjnego za blok | 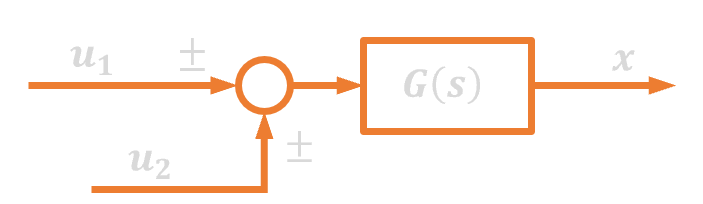 |
 |
| 8. | Przesuwanie węzła sumacyjnego przed blok | 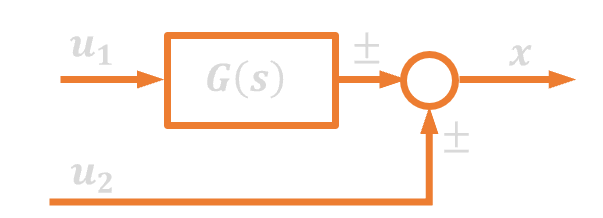 |
 |
| 9. | Zamiana kolejności węzłów zaczepowych | 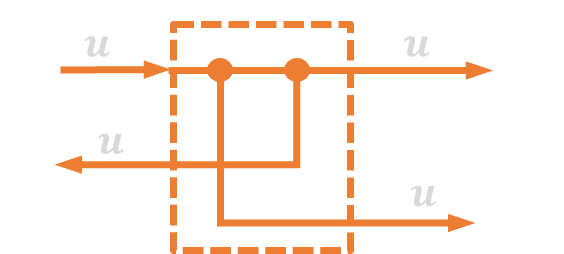 |
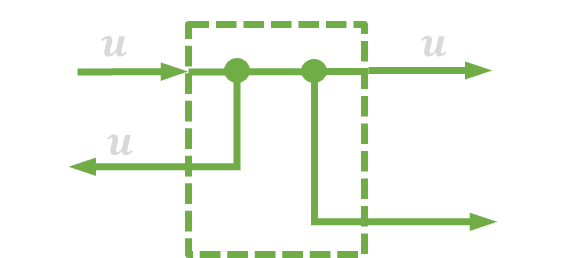 |
| 10. | Łączenie/rozdzielanie węzłów sumacyjnych | 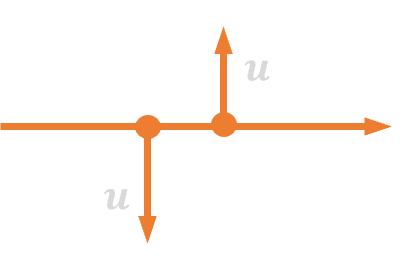 |
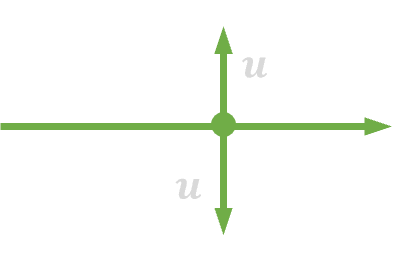 |
| 11. | Zamiana kolejności węzłów zaczepowych | 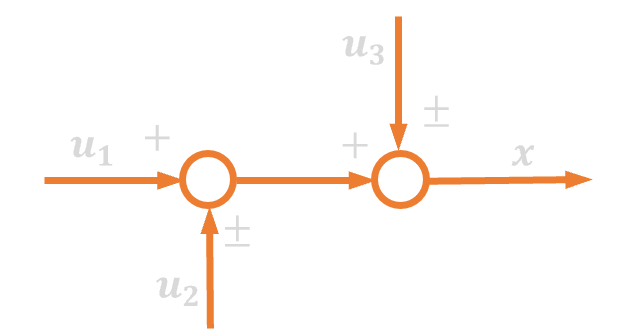 |
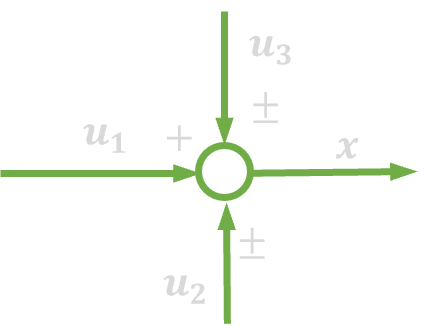 |
| 12. | Zamiana kolejności węzłów sumacyjnych | 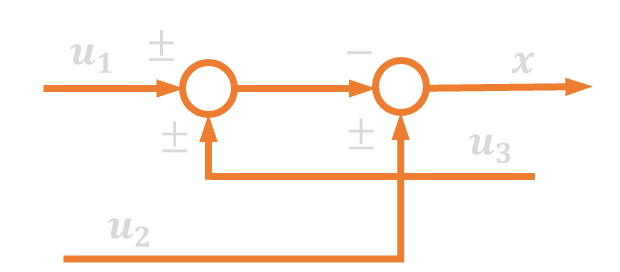 |
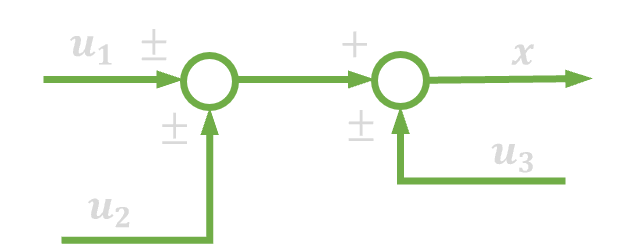 |
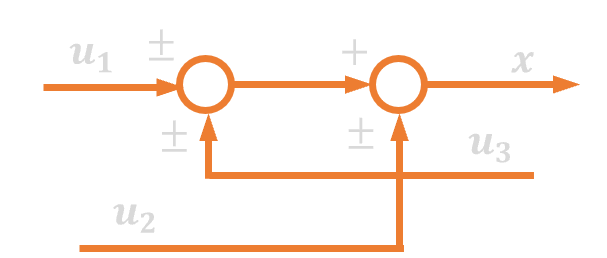 |
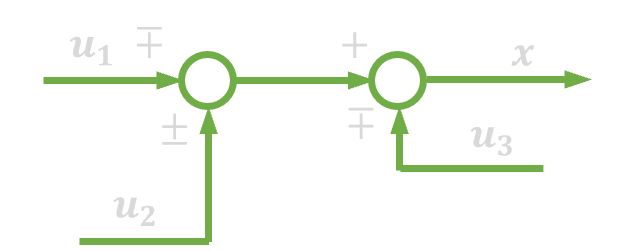 |
||
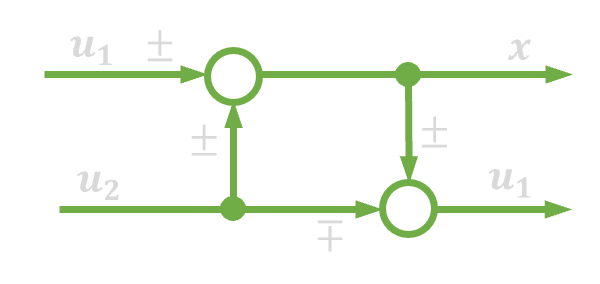
| 13. | Zamiana kolejności węzła zaczepowego i sumacyjnego | 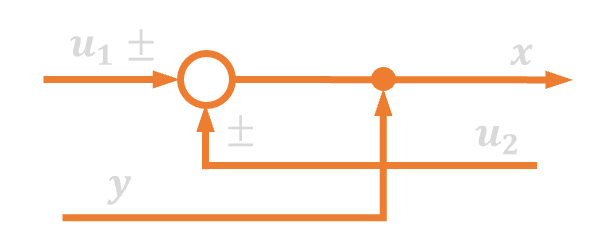 |
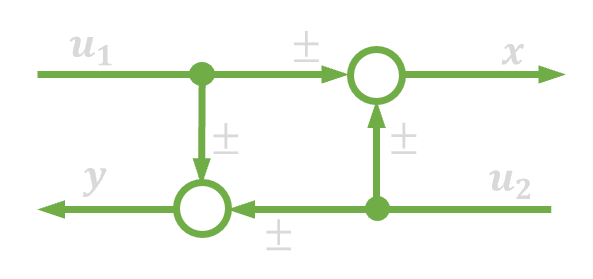 |
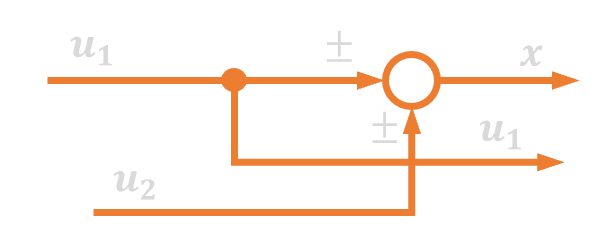 |
 |
Literatura:
[1] Klimasara W., Pilat Z.: Podstawy automatyki i robotyki, Wydawnictwo Szkolne i Pedagogiczne, 2006 r, ISBN: 978-8-302094-23-1.
[2] Gupta A.K., Arora S.K., Westcott J.R.: Industrial automation and robotics, Mercury Learning and Information, 2016, ISBN: 978-1-942270-04-1.
[3] Dorf R.C, Bishop R.H.: Modern control systems, Prentice Hall, 12 edycja, ISBN 978-0-13-602458-3.
[4] Czemplik A.: Modele dynamiki układów fizycznych dla inżynierów, Wydawnictwo WNT, 2017, ISBN 978-83-01-19520-5.
Ocenianie